CMPSCI 653: Sample Exam Problems
Note: The exam will consist of two kinds of
questions. A question can require you to analyze protocols or
algorithms that we discussed on class (or simple variants
thereof). The other kind of question will require you to design
protocols/algorithms satisfying a particular property (similar to the
ones we have discussed in class). This document consists of sample problems
illustrating both kinds of questions.
Slotted Aloha
Suppose that N stations share a slotted Aloha channel and that they always
have a packet to transmit. Assume that each station attempts to transmit a
packet in a slot with probability p.
- What is the probability that the channel is idle during a slot?
- What is the throughput, i.e., the probability that a successful
transmission occurs during a slot (one packet is transmitted)?
- Find the value of p that maximizes the channel throughput.
- Using the value of p determined above, find the throughput of slotted
Aloha by letting N approach infinity. Hint: (1-1/N)^N approaches 1/e as N
approaches infinity.
Split Horizon Algorithm
We saw that the split horizon algorithm can sometimes used to avoid the
"count to infinity" problem. Give an example showing that the split
horizon does not always solve the count to infinity problem.
Minimum Average Delay Routing
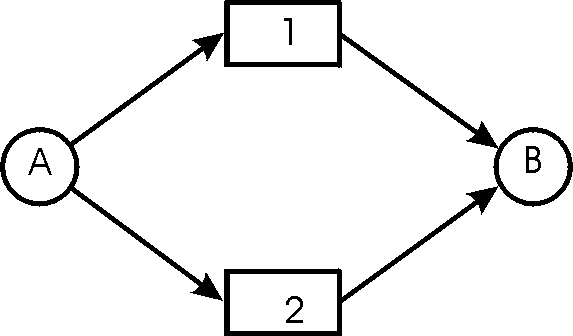
Consider the following routing problem. Packets have a choice of one of
two routes between A and B. Assume that in each case, there is only one link.
Let a denote the packet arrival rate at A and B_1 and
B_2 the two link bandwidths (bits/sec)
For the moment, consider link i. Assume that it is offered packets at
rate a_i packets per second, the mean packet length is l bits,
and the bandwidth of the link is B_i bits per second. Under suitable
assumptions, the average packet delay (time waiting in the buffer plus
transmission), is given as
T_i = l/(B_i-a_i l)
when a_i < B_i/l and infinity otherwise.
We have computed the average packet delay for route i, T_i. The
average delay seen by any packet is
T = (a_1 T_1 + a_2 T_2)/a
Now consider a routing algorithm that
splits the traffic between the
two routes in such a way as to minimize the average packet delay. Let p
denote the probability that a packet goes over route 1 and 1-p the
probability
that a packet goes over route 2. Hence the arrival rates to the two links are
a_1 = pa and a_2 = (1-p)a respectively. Using the formula above,
the overall average packet delay is given as
T = p l/(B_1 - p a l) + (1-p) l/(B_2-(1-p)a l).
Answer the following:
- What is the value of p that minimizes T? Be careful that
p satisfies
0 <=p <=1.
- Take l = 1000 bytes and a = 1000 pkts/sec. Plot (a) the
average delay
of packets, and (b) the optimal value of p that achieves this
for the above algorithm as a function of B_1 in the range
[0MBs, 2MBs] where B_2 = 2MBs - B_1.
A NAK-based Protocol
Design a reliable, pipelined, data transfer protocol that uses only negative
acknowledgements. How quickly will your protocol respond to lost
packets when the arrival rate of data ot the sender is low? Is high?
You may assume an infinitely large sequence number space, that
the channel may lose or corrupt messages,
and that delays are variable and unknown.
Last, can you think of any advantage of a NAK-based protocol?
Design your own protocol
Design an application-level protocol to be used between a client
process running on a travel agent's desktop computer and a
centralized (server) process which controls an airline's
reservation system. Your protocol should allow the client to
request a flight schedule between two cities on a given date.
The client should also be able to book a seat on a flight,
specifying the passenger's credit card number to pay for the
flight. The client should also be able to cancel a reservation
Your protocol server entity should be able to handle various
error scenarios (e.g., flight information for a city without an
airport, booking a flight that is sold out, canceling a non-existent
reservation, an invalid credit card number, etc.).
Explicitly state your assumptions about the underlying presentation,
and data transport services.
You can specify your protocol by
listing the types of messages to be sent from the agent
to the airline's server, and vice versa. For each message type,
specify any additional data fields required.
Your design should also specify for each agent message, the possible
server replies, and for each server reply,
the possible client actions.
Sketch a scenario
for the case in which a flight information is requested, and
reservation is made and paid for. Also sketch a scenario in which
an error condition of your own choosing is detected and handled.
Prashant Shenoy
Last modified: Sun Apr 2 12:17:31 EDT 2000

